SÁCH GIÁO KHOA
1. GÓC Ở VỊ TRÍ ĐẶC BIỆT
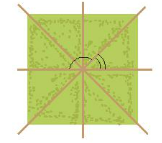
Hoạt động 1: Quan sát hình vẽ bên. Em hãy nhận xét về mối quan hệ về đỉnh, về cạnh của hai góc được đánh dấu.
Hướng dẫn giải:
2 góc được đánh dấu là 2 góc có:
- chung đỉnh
- chung một cạnh
- cạnh còn lại là 2 tia đối nhau
Hoạt động 2: Cho ba tia Ox, Oy, Oz như Hình 3.1, trong đó Ox và Oy là hai tia đối nhau.
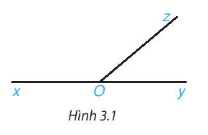
a) Em hãy nhận xét về quan hệ về đỉnh, về cạnh của hai góc xOz và zOy.
b) Đo rồi tính tổng số đo góc hai góc xOz và zOy.
Hướng dẫn giải:
a.Đỉnh của góc xOz và zOy cùng là đỉnh O
2 góc xOz và zOy có chung cạnh Oz, cạnh còn lại (Ox và Oy) là 2 tia đối nhau
b.
- \(\widehat{xOz}\) = 135\(^{\circ}\)
- \(\widehat{yOz}\) = 45\(^{\circ}\)
=> \(\widehat{xOz}\) + \(\widehat{yOz}\) = 135\(^{\circ}\)+ 45\(^{\circ}\) = 180 \(^{\circ}\)
Câu hỏi 1: Hai góc được đánh dấu trong hình nào dưới đây là hai góc kề bù?
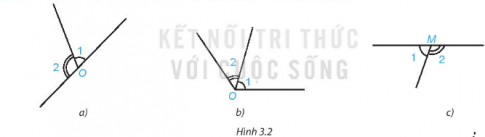
Hướng dẫn giải:
Hình a và c.
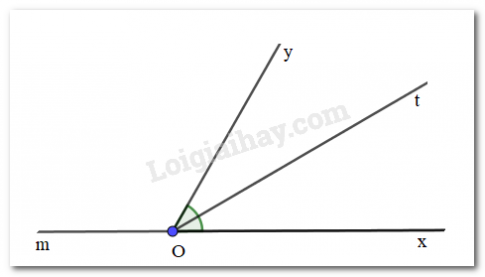
Luyện tập 1: Viết tên hai góc kề bù trong Hình 3.4 và tính số đo góc mOt
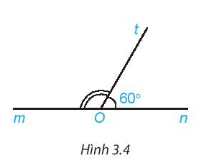
Hướng dẫn giải:
2 góc kề bù trong hình là: góc mOt và tOn
\(\widehat{mOt}\)= 180\(^{\circ}\) - \(\widehat{nOt}\)= 180\(^{\circ}\) - 60\(^{\circ}\)= 120\(^{\circ}\)
Hoạt động 3: Quan sát hình ảnh hai góc được đánh dấu trong hình bên. Em hãy nhận xét quan hệ về đỉnh, về cạnh của hia góc được đánh dấu.
Hướng dẫn giải:
2 góc trên hình có :
- cùng đỉnh
- từng cạnh của góc này là tia đối của cạnh của góc kia.
Hoạt động 4: Cho hai đường thẳng xx’ và yy’ cắt nhau tại O (H.3.5)
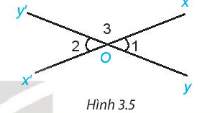
a) Dự đoán xem hai góc xOy và x’Oy’ có bằng nhau không?
b) Đo rồi so sánh số đo hai góc xOy và x’Oy’
Hướng dẫn giải:
a. Theo em thì hai góc xOy và x’Oy’ có bằng nhau.
b. \(\widehat{xOy}\) = \(\widehat{x'Oy'}\) =31\(^{\circ}\)
Câu hỏi 2: Hai góc được đánh dấu trong hình nào dưới đây là hai góc đối đỉnh?
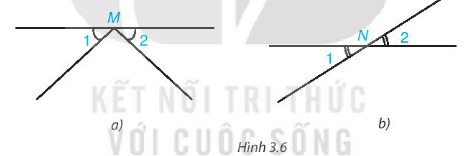
Hướng dẫn giải:
2 góc ở hình 3.6.b là hia góc đối đỉnh vì 2 góc này có mỗi cạnh của góc này là tia đối của một cạnh của góc kia.
Luyện tập 2: Hai đường thẳng xx’ và yy’ cắt nhau tại O sao cho góc xOy vuông (H.3.8). Khi đó các góc yOx’, x’Oy’, xOy’ cũng đều là góc vuông. Vì sao?
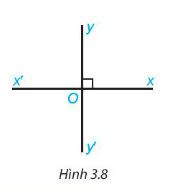
Hướng dẫn giải:
- \(\widehat{xOy}\) và \(\widehat{x'Oy'}\) là hai góc đối nhau nên \(\widehat{xOy}\) + \(\widehat{x'Oy'}\) = 180\(^{\circ}\)
\(\widehat{xOy}\) và \(\widehat{xOy'}\) là hai góc kề bù nên \(\widehat{xOy}\) + \(\widehat{xOy'}\) = 180\(^{\circ}\)
=> \(\widehat{xOy'}\) = 180\(^{\circ}\)- \(\widehat{xOy}\) = 180\(^{\circ}\) - 90\(^{\circ}\) = 90\(^{\circ}\)
- \(\widehat{x'Oy}\) và \(\widehat{xOy}\) là hai góc đối nhau nên \(\widehat{x'Oy}\) + \(\widehat{xOy}\) = 180\(^{\circ}\)
2. TIA PHÂN GIÁC CỦA MỘT GÓC
Hoạt động 5: Cắt rời một góc xOy từ một tờ giấy rồi gấp sao cho hai cạnh của góc trùng nhau (H.3.9).
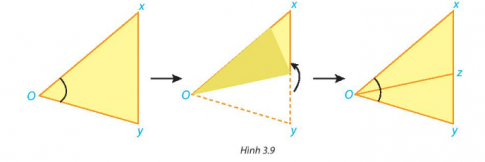
Mở mảnh giấy ra, nếp gấp cho ta hình ảnh tia Oz chia góc ban đầu thành hai góc.
a. Em hãy nhận xét về vị trí của tia Oz so với hai cạnh của góc xOy.
b. Em hãy so sánh hai góc xOz và zOy.
Hướng dẫn giải:
a. Tia Oz nằm giữa hai cạnh của góc xOy.
b. \(\widehat{xOz}\) = \(\widehat{zOy}\).
Luyện tập 3: Cho góc xAm có số đo bằng \(65^{\circ}\) Am là tia phân giác của góc xAy (H.3.12). Tính số đo góc xAy
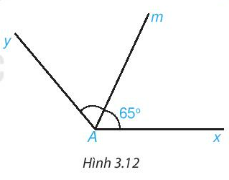
Am là tia phân giác của góc xAy => \(\widehat{xAm}\)= \(\widehat{mAy}\)= \(\frac{1}{2}\)\(\widehat{xAy}\)
=>\(\widehat{xAy}\) = 2. \(\widehat{xAm}\) = 2. \(65^{\circ}\) = \(130^{\circ}\)
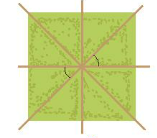
Vận dụng: Quan sát hình vẽ bên.
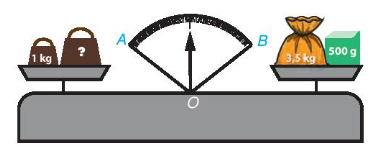
Hướng dẫn giải:
Đổi 500 g = 0,5 kg
- Tổng cân nặng bên đĩa cân phải là: 3,5 + 0,5 = 4(kg)
Để cân thăng bằng thì quả cân ở đĩa cân bên trái nặng số kilogam là: 4 – 1 = 3 (kg)
Bài 3.1 trang 45 toán 7 tập 1 KNTT
Cho Hình 3.13, hãy kể tên các cặp góc kề bù.
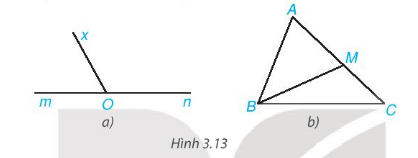
Bài 3.2 trang 45 toán 7 tập 1 KNTT
Cho Hình 3.14, hãy kể tên các cặp góc đối đỉnh.
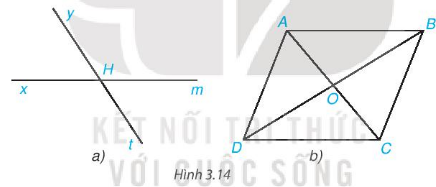
Bài 3.3 trang 45 toán 7 tập 1 KNTT
Vẽ góc xOy có số đo bằng \(60^{\circ}\). Vẽ tia Om là tia đối của tia Ox.
a. Gọi tên hai góc kề bù có trong hình vừa vẽ.
b. Tính số đo góc yOm.
c. Vẽ tia Ot là tia phân giác của góc xOy. Tính số đo các góc tOy và tOm.
Bài 3.4 trang 45 toán 7 tập 1 KNTT
Cho Hình 3.15a, biết \(\widehat{DMA}\) = \(45^{\circ}\). Tính số đo \(\widehat{DMB}\)
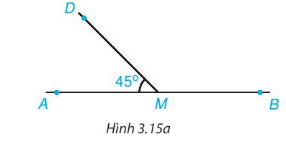
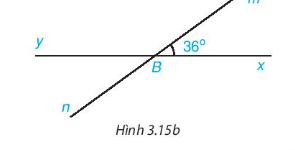
Bài 3.5 trang 45 toán 7 tập 1 KNTT
Cho Hình 3.15b, biết \(\widehat{xBm}\) = \(36^{\circ}\). Tính số đo các góc còn lại trong hình vừa vẽ.